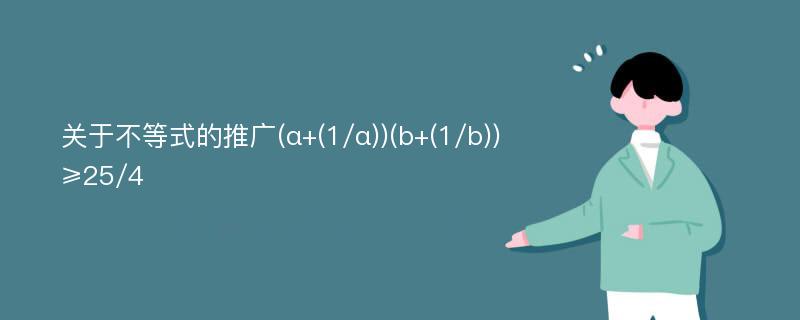
一、再论不等式(α+(1/α))(b+(1/b))≥25/4的推广(论文文献综述)
中学数学教学参考试题研究组[1](2003)在《2002年全国各地数学高考模拟试题集锦》文中研究指明
李建磊[2](2010)在《大型稀疏代数系统的数值求解研究》文中认为科学与工程计算的很多领域,诸如计算流体力学、约束优化、计算电磁学、PDEs的混合有限元近似、非线性规划、中子输运理论等问题的求解,最终都可归结为大型稀疏代数系统的求解.因此,对大型稀疏代数系统的求解研究就具有非常重要的理论意义和实际应用价值.由于许多实际问题产生的大型稀疏代数系统往往具有某种特殊结构,对具有这些特殊结构的大型稀疏代数系统的数值求解研究引起了国内外众多专家和学者的关注.本文对几类特殊的大型稀疏代数系统的数值求解方法进行了深入系统地研究.特别研究了求解线性鞍点问题的迭代法和预处理技术,求解非线性鞍点问题的迭代法以及求解代数黎卡提方程的迭代法.本文共六章,分四个部分:研究求解线性鞍点问题的Uzawa类迭代法.首先,提出了一个修正的非线性Uzawa迭代法,讨论了算法的收敛性,并给出了理论和数值比较,数值实验也验证了修正方法的有效性.其次,给出了求解(2,2)块不为零的非对称广义鞍点问题的GMLHSS迭代方法,并探讨了算法的收敛条件.最后,给出了非精确Uzawa方法、GSSOR方法和MLHSS方法求解奇异鞍点系统时的半收敛性分析.研究求解非对称鞍点问题的预处理技术.首先,给出了含参数的广义非精确块三角预条件子,对预处理矩阵的特征对性质给出了分析,并给出了预处理矩阵的特征值扰动分析.其次,基于系数矩阵的部分HS分裂和PS分裂,提出了PHSS预条件子和PPSS预条件子,并详细研究了预处理矩阵的谱性质,指出对于一个充分小的正参数,预处理矩阵特征值聚集在两个点附近:一个是(0,0)点,另一个是(2,0)点,并且通过大量的数值实验验证了理论分析和此两类预条件子的有效性.最后,给出了SIMPLE预条件子,利用特征值理论,研究了预处理矩阵两种不同表达形式的谱之间的联系.研究求解非线性鞍点问题的迭代法.在求解线性鞍点问题的迭代解法基础上,给出了几个求解非线性鞍点问题的迭代法,并对方法进行了收敛性分析,数值实验验证了所提算法的有效性.研究求解代数黎卡提方程的迭代法.事实上,输运理论中的代数黎卡提方程可以写成与之等价的向量方程.首先,基于松弛思想和牛顿方法,提出了求解向量方程的松弛Newton-like方法,并给出了算法的收敛性分析.其次,利用拟牛顿思想,结合已有的牛顿类型方法,给出了两个修正牛顿方法求解向量方程,并得到了算法的收敛结果.数值实验也表明所给出的三个算法能有效改进和提高已有算法的收敛性.
吴善和[3](2006)在《一类新的Radon型不等式及其应用》文中研究表明给出一类新的R adon型不等式,它们在代数不等式研究中有着广泛的应用,利用它们可直接得到一大批新的分式型不等式,也可运用它们证明或推广许多不等式.
涂智瑜,刘春燕,罗佩,张如庆,蔡金婷,刘小松[4](2015)在《Cn中单位多圆柱上一类α型螺形映射齐次展开式第四项的精确估计》文中提出本文主要给出Cn中单位多圆柱上一类正规化双全纯螺形映射第四项齐次展开式的精确估计,所得结果揭示在一定的限制条件下关于α型螺形映射齐次展开式第四项的多复变数Bieberbach猜想成立,从而推广了多复变数已有的结果.
路坤锋[5](2014)在《空间飞行器姿态复合控制方法研究》文中指出姿态控制是空间飞行器完成各种任务的前提和保障。在空间飞行器执行任务过程中,姿态动力学系统不仅具有强烈的非线性,而且会受到转动惯量不确定和外部环境扰动的影响。此外,在实际应用中控制输入饱和和执行器故障也应加以考虑。近年来,随着空间飞行器结构和任务的日益复杂,对飞行器控制算法的要求也越来越高,单一的控制算法无法解决在内部不确定和外部扰动影响情况下,飞行器姿态控制系统的多指标优化控制问题。本文以滑模控制为基础分别结合扩张状态观测器(ESO)、微分观测器(DO)、鲁棒控制和自适应控制,构造几种复合控制策略来同时满足系统的快速性、精确性、鲁棒性,甚至低能量消耗等多指标的要求。本文完善了终端滑模控制、二阶Super-twisting算法和抖振抑制技术,首次完成了终端滑模结合自适应复合控制方案的有限时间稳定证明。论文的主要内容如下:1.研究了转动惯量不确定、外部扰动和执行器饱和情况下空间飞行器快速、高精度姿态跟踪控制问题。通过数学变换得到了更优化的空间飞行器动力学模型,其不仅减轻了观测器的负担,而且提高了控制器的精度。设计了滑模控制结合观测器估计的复合控制方案。利用观测器(ESO或DO)对飞行器系统总不确定项进行精确估计,再利用滑模控制和反步控制技术的快速响应,实现空间飞行器高性能姿态跟踪控制。而且,滑模控制技术的快速响应弥补了观测器估计能力有限的问题;反过来,观测器的精确估计能力又抑制了滑模高频抖振现象的产生。2.研究了基于非奇异终端滑模技术的空间飞行器有限时间姿态稳定问题。首先,设计了鲁棒非奇异终端滑模控制方案,保证空间飞行器姿态系统有限时间稳定且避免奇异问题。然后,提出了自适应非奇异终端滑模复合控制方案。该方案一方面利用自适应技术对不确定和扰动的上界进行估计和补偿,另一方面,利用非奇异终端滑模的快速性和强鲁棒性,从而实现飞行器系统的有限时间姿态稳定。由于自适应滑模控制方案不依赖转动惯量不确定和外部扰动的任何信息,该方案可以应用于难以获取这些信息的实际系统中。自适应技术的精确估计和补偿能力有效抑制了滑模控制中的抖振问题。本文首次完成了基于自适应非奇异终端滑模控制方案的飞行器姿态系统有限时间姿态稳定的严格证明,并得到了有限收敛时间上界的估计值。3.研究了基于快速非奇异终端滑模技术的空间飞行器有限时间姿态跟踪控制问题。设计的快速非奇异终端滑模面同时包含了线性滑模面和非奇异终端滑模面的优点。然后,将快速非奇异终端滑模控制技术和自适应控制技术结合,设计了五种空间飞行器姿态跟踪控制方案,实现了飞行器系统的有限时间全局姿态跟踪控制,避免了奇异问题,抑制了抖动现象,摆脱了控制方案对转动惯量不确定和外部扰动信息依赖的限制。本文还提出了一种处理抖振问题的新技术。根据Lyapunov稳定定理和有限时间技术,首次完成了自适应快速非奇异终端滑模控制方案有限时间姿态跟踪控制的严格证明,得到了收敛域上界的精确估计值,给出了参数调节的理论依据。4.基于“等价控制”思想,研究了具有低能量消耗的空间飞行器有限时间姿态跟踪控制问题。设计了自适应增益Super-twisting算法和自适应增益快速终端滑模控制方案。设计的控制律实现了飞行器系统的精确定位、快速响应和强鲁棒性并保证了低能量消耗。控制方案解决了滑模控制带来的抖振和高频切换问题。跟经典Super-twisting算法相比,改进的Super-twisting控制算法包含如下优点:1)不依赖不确定和扰动上界的先验信息;2)完成了对随时间和状态变化的外部扰动和内部不确定的有效抑制;3)自适应增益解决了超调问题及控制增益选取困难问题;4)加入了纠正项保证了更快的收敛速度。本文还分别给出了基于自适应增益Super-twisting算法和自适应增益快速终端滑模控制算法的飞行器系统有限时间姿态跟踪控制的严格证明,得到了有限收敛时间上界的估计值和收敛域上界的精确表达式。控制方案包含了快速趋近律技术、Super-twisting算法和自适应技术的优点。5.在转动惯量不确定、外部扰动、执行器故障和执行器饱和影响空间飞行器系统情况下,研究了有限时间容错姿态控制问题。第一部分:研究了有限时间容错姿态稳定控制问题。设计的鲁棒(自适应)控制方案保证了系统轨迹在有限时间内收敛到滑模面上,然后在有限时间内收敛到平衡点附近的小邻域。利用实用滑模概念,对自适应快速终端滑模控制律进行了改进以满足其在实际工程中的需要。提出的控制方案实现了有限时间容错控制,保证姿态控制系统的高性能品质,并给出了有限时间容错姿态稳定的严格证明。第二部分:提出了基于快速终端滑模和自适应技术的复合控制方案,解决了空间飞行器系统的有限时间容错姿态跟踪控制问题。在不需要故障诊断获取故障信息的情况下,该方案实现了有限时间容错控制;在不需要转动惯量不确定和外部扰动先验信息的情况下对其保持了强鲁棒性。本文用两种方式描述了执行器饱和问题,提出了一种处理仿射非线性系统总不确定项的新技巧。在转动惯量不确定、外部扰动、执行器故障和执行器饱和影响飞行器系统的情况下,首次完成了有限时间容错跟踪控制的严格证明,给出了收敛域上界的精确表达式,得到了有限收敛时间、收敛域和执行器故障和执行器饱和度之间关系的表达式。6.仿真实例验证了控制方案的合理性和有效性。对比仿真验证了控制方案的优越性。采用实际卫星数据的数值仿真验证了控制方案的实用性。最后,归纳总结了本论文的主要研究成果,并对今后的工作进行了展望。
苏贵福[6](2014)在《关于图的拓扑不变量和结构性质的几个问题》文中指出图论与化学有史以来就有着非常紧密的联系,化学结构可以很简单地表示成图(化学图或分子图)的形式.拓扑指标是理论化学中的一种拓扑不变量,它们是一些不依赖于图的标号和画法的实数.为了更好的研究分子的性质,数学家和理论化学家提出了很多拓扑指标并获得很多重要深刻的结果.本论文以图的拓扑指标为主线展开讨论.第一部分是对本论文所涉及问题的背景,进展以及所得结果的一个综述.以下五部分为本论文的主要贡献:定义κ(G):=κ, λ(G):=λ, δ(G):=δ.1932年在[H. Whitney, Congruent graphs andthe connectivity of graphs, Amer. J. Math.54(1932)150-168]中证明了一个着名的定理:对任意的图G,有κ≤λ≤δ.随后判断一个图是否是极大边连通的(λ=δ)问题得到很多学者的关注[A. Hellwing, L. Volkmann, Maximally edge-connected and vertex-connectedgraphs and digraphs: A survey, Discrete Math.308(2008)3265-3296].第二章我们借助广义零阶Randic′指标(R0α)证明了:当α≤1且R0α(G)<2δα δα+1+(δ1)(δ+1)α+(δ1)(n δ1)α+(2n3δ2)(n δ2)α时,图G是极大边连通的;若图G中不含三角形,当R0+1α(G)<δα δα+(δ1)(δ+1)α+2α(δ1)(n2δ+2)α+2α(2n5δ+1)(n2δ)α时,图G是极大边连通的.我们的结果推广了[P. Dankelmann, A. Hellwig, L. Volkmann,Inverse degree and edge-connectivity, Discrete Math.309(2009)2943-2947]中给出的定理.当0<α <1时我们证明了类似的结论并刻画了相应的极图(定理2.2.1和定理2.2.2).最后我们获得判断一个图是超边连通的充分条件(定理2.3.6)并推广了[Y. Tian, L. Guo, J.Meng, C. Qian, Inverse degree and super edge-connectivity, International Journal of Comput.Math.89:6(2012)752-759]中的一个定理.问题2.3.8和问题2.3.9是我们未来旨在解决的两个主要问题.设Q是图G的任意拓扑不变量,在第三章我们提出图的[Q,k]-分解问题的概念,着重研究图的H-指标, WW-指标, R0α-指标, RDD+-指标, RDD-指标以及χα-指标的[Q,k]-分解问题.获得了八个诸如7(n)2≤WW(3; Kn)≤2(n+2)4+(n)2+4(n1)的最好可能的结果.我们的结果(定理1.36)实质性地推广了[L. Zhang, B. Wu, The Nordhaus-Gaddum-type inequalities for some chemical indices, MATCH Commun. Math. Comput. Chem.54(2005)189-194]中给出的定理.本章还提出几个进一步研究的问题(猜想3.2.17等).第四章我们首先给出了图的Co-PI指标的等价定义并研究其基本性质.在此基础上刻画了图的笛卡尔积的Co-PI谱半径并得到如下结果: σ′kl(G1G2)=|V1|σ′l(G2)+|V2|σ′k(G1)和μ′kl(G1G2)=|V1|μ′l(G2)+|V2|μ′k(G1),其中k=1,2,···,|V1|并且l=1,2,···,|V2|.同时我们给出第二和第三阶Co-PI谱距的上下界.最后利用Co-PI指标的等价定义推导出图的笛卡尔积的Co-PI指标的精确表达式(定理4.3.1和定理4.3.3).第五章我们介绍了图的可Q-最大最小化问题的概念,并证明了当图的点连通度κ给定时,有RDD (G)≤21n4217n3+21(κ3κ2+3κ+18)n2+21(κ311κ20)n+21(κ2+9κ+8),这里的结果是最好可能的.当匹配数β给定时我们研究了图的可RDD+-最大化和可RDD-最大化问题(定理5.1.3和定理5.2.9).最后我们也考虑了独立数α给定时图的可RDD+-最大化问题,并确定了达到此上界的极图(定理5.3.4).第六章讨论了Tadpole图,轮图以及梯形图的剖分的线图的几种拓扑指标的计算公式,我们的结果推广了[P. S. Ranjini, V. Lokesha, I. N. Cangu¨e, On the Zagreb indices of theline graphs of the subdivision graphs, Appl. Math. Comput.218(2011)699-701]中获得的几个定理.
邓明宇[7](2020)在《非线性系统的广义张量方法》文中进行了进一步梳理近几年来,由于人工智能、神经网路的的兴盛,非线性系统的求解再度成为科学和工程计算领域中比较热门的话题之一,受到了较大的关注.本文提出了求解大型非线性系统的一种新的张量方法(广义张量方法),方法的重点是每一步内迭代需求解张量方程.首先,对于弱非线性张量方程,本文分析了其系数矩阵是否为零矩阵的两种情形,并提出基于HSS迭代(如Newton-HSS、Picard-HSS以及nonlinear HSS-like方法)的求解方法.理论分析表明,在合理的假设下这些方法是局部收敛的.数值结果显示:当系数矩阵为零矩阵时,Newton-HSS方法优于Newton-GMRES方法?而当系数矩阵为非零矩阵时,基于HSS迭代的方法较为高效、稳定,尤其是nonlinear HSS-like方法的效果更优.其次,对于多维线性.系统(非线性)的特殊情形,对称M-系统,基于Picard与非线性迭代的思想,本文给出了HSS-D、HSS-F两种方法并进行了局部收敛性的分析,数值实验表明HSS-D方法要优于现有的迭代方法,而HSS-F方法比现有的部分方法好,但有一定局限性.再其次,从理论上证明了非齐次M-方程的正根的存在唯一性,给出了广义张量方法的近似收敛阶.最后,提出了广义张量方法的三种非精确形式:Tensor-Picard CG(T-P CG),Tensor-Picard GMRES(T-P GMRES)和Tensor-nonlinear HSS(T-N HSS)方法,数值例子表明T-P CG方法是最优,基本上优于其两种方法以及已有的Newton-HSS、Newton-GMRES方法.
丁锋[8](2011)在《系统辨识(3):辨识精度与辨识基本问题》文中指出系统辨识是研究建立系统数学模型的理论与方法.讨论系统辨识涉及的一些基本问题,包括辨识精度、辨识方法的提出,辨识输入信号的设计,参数可辨识性与系统可辨识性,开环可辨识性与闭环可辨识性,可辨识性与能控性和能观测性的关系,可辨识性与输入信号的关系,以及与辨识方法收敛性相关的激励信号与激励条件,辨识算法收敛分析的基本工具,典型辨识算法的收敛结论等.
张波[9](2016)在《忆阻系统的同步及其控制研究》文中研究指明忆阻是华人电路理论专家蔡少棠教授首次提出的概念.忆阻器被假设为与电量和磁通量相关的,消失的非线性无源二终端电路元件.自其被提出后的近四十年间,忆阻的研究几乎没什么突破性进展.直到2008年,惠普实验室制作出第一款忆阻器,其便引起了许多科研人员的注意,迅速地成为了自动化等相关领域最热门的研究方向之一.忆阻对流经其的电流或两端的电压具有独特的记忆功能,其应用前景十分广泛,如在保密通信、存储器、人工智能计算机等众多领域都具有巨大的潜在应用价值.据目前已有的文献来看,国际上对忆阻的研究主要集中在两个方面:(1)按照惠普实验室研究的思路,研究如何以最经济实惠的材料制作出具有忆阻特性的器件;(2)按照蔡少棠教授的思路,研究由忆阻构建的系统的动力学行为及其应用.本文按照蔡少棠教授的思路,继续对忆阻系统的动力学行为及其应用进行了更深入的研究,包括忆阻系统的同步以及控制.研究的对象涉及已有大量文献报道的忆阻神经网络和忆阻混沌系统等.笔者还考虑了忆阻系统与随机系统相结合,如利用间歇随机扰动镇定忆阻混沌系统;忆阻系统与不连续系统理论相结合进一步研究了忆阻系统的动力学性质.我们利用动力系统理论的一些基本工具,如Lyapunov稳定性理论、Hanalay不等式、脉冲理论等现代控制理论方法,也将利用随机系统的Lyapunov稳定性理论等随机系统中的常用方法.通过对上述问题和方法的研究,建立了忆阻系统的同步以及控制研究的基本结构,在忆阻的理论和应用的研究上取得了一定进展.本文的主要贡献阐述如下:1.介绍了忆阻的相关背景、研究意义和现状,着重阐述了忆阻神经网络和忆阻混沌系统的研究进展,简单介绍了与本文相关的理论知识.2.基于四个混沌系统的组合-组合同步和复合同步,研究了一种六个忆阻Lorenz系统的新型双复合同步.利用Lyapunov稳定性理论和状态反馈控制方法,得到了确保结论成立的充分条件,并且进行了相应的理论证明和数值仿真,验证了我们的同步设计方法的有效性和可行性.由于所设计的同步复杂性更高,因此在通讯应用中,传递和接收信号的安全性更好.3.研究了基于忆阻Lorenz系统的离散和分布时变时滞随机混沌系统的混合控制问题.首先,基于由分段线性忆阻建模的Lorenz系统,提出了一个随机切换混沌系统.其次,设计一个新型混合控制器,并建立保证相应的随机系统平凡解均方指数稳定的判据.此外,本文提出了一个新技术,解决了两个不同时刻所对应的状态值之差的问题,而这两个时刻之间可能存在脉冲时刻,其对应的状态值之差不能直接用随机Newton-Leibniz公式来刻画.最后,给出数值例子证明了设计方法的有效性和可行性.4.考虑了基于间歇布朗噪声扰动对一个给定的非线性系统的镇定与消稳问题.首先,给出了一些与控制周期T和噪声宽度δ相关的新型稳定性与不稳定性判据和结论.随后利用所得到的结果研究基于间歇随机扰动的镇定与消稳,并且把所获得的理论应用于忆阻混沌系统的镇定问题.最后给出两个数值例子验证了我们的理论.5.研究了基于分布脉冲控制的随机时滞忆阻神经网络的指数同步问题.根据忆阻的特性,建立了相应的驱动随机忆阻神经网络和具有分布脉冲控制输入的响应随机忆阻神经网络,再利用同步的概念和随机微分包含理论得到了同步误差系统.利用广义脉冲时滞微分不等式方法,我们得到同步误差系统均方指数稳定的判据,即驱动系统和相应系统达到指数同步的判据.最后给出了数值仿真验证了所得理论结果的有效性.最后,总结本文工作,展望后续课题.
李建雄[10](2012)在《轧机电液伺服系统的鲁棒自适应输出反馈控制研究》文中进行了进一步梳理对于电液伺服系统的高精度控制问题,目前已经取得了较为丰富的研究成果,然而,这些成果绝大部分是在假设所有状态可测量的情况下,采用状态反馈取得的,输出反馈的成果却很少。在电液伺服系统的许多应用场合都存在不可测状态,如柱塞速度信号、加速度信号,因此,研究电液伺服系统的输出反馈控制是非常必要的。本课题结合河北省自然科学基金“液压伺服驱动的冷带轧机厚控系统自适应鲁棒控制研究”和国家自然科学基金“考虑输入受限的轧机液压伺服系统多模型切换自适应控制研究”,以轧机电液伺服系统为研究对象,针对系统中普遍存在的状态不可测、参数不确定、非线性、外负载力未知、输入饱和,以及轧机厚控系统存在的测量延时等问题进行了鲁棒自适应输出反馈控制方面的研究。本文主要做了以下几方面工作:首先,针对轧机电液伺服位置系统中存在不确定参数和未知外负载力,提出了一种基于未知输入降维观测器的鲁棒输出反馈控制算法。将包含未知外负载力的干扰项视为系统的未知输入,构造未知输入降维观测器用于估计系统的不可测状态和未知干扰项,进而,基于所得到的估计值设计输出反馈控制器。与传统的输出反馈控制算法相比较,本文提出的算法具有更好的暂态性能和更小的稳态误差。其次,针对轧机电液伺服位置系统中存在不确定参数,在假设不确定参数上界已知的情况下,提出了一种基于高增益观测器和参数估计器的自适应输出反馈控制算法。通过选取适当的设计参数,该算法能够保证闭环系统的所有信号最终有界,系统状态及其估计值最终收敛到原点的一个由高增益决定的邻域内;对于不确定参数上界未知的情况,并考虑一些未建模动态,可将电液伺服位置系统视为具有未知控制系数和未知线性增长率的非线性系统。对这样一类系统,提出了一种基于动态高增益观测器的自适应输出反馈控制算法。在该算法中,利用线性组合变换,使得变换后的广义误差的动态不再依赖于控制输入,以便于输出反馈控制器设计;通过引入动态高增益,解决了系统线性增长率未知的问题。该算法能够保证闭环系统所有信号有界,且系统状态和估计误差最终收敛到零。进而,将该算法应用到电液伺服位置系统中,并通过实例仿真验证了该算法的有效性。第三,考虑到轧机电液伺服位置系统中存在的输入饱和,给出了一种抗饱和鲁棒动态输出反馈控制算法。首先在不考虑输入饱和情况下设计鲁棒动态输出反馈控制器,利用Finsler引理将保证闭环系统稳定的充分条件转化为线性矩阵不等式(LMI)条件,通过求解LMI可得到控制器参数矩阵。然后基于anti-windup方法设计了抗饱和鲁棒动态输出反馈控制器。所设计的控制器能够保证闭环系统有界稳定,并具有鲁棒H∞性能。最后,考虑到轧机厚控系统的输出测量存在延时,给出了一种基于观测器的输出反馈鲁棒预测控制算法。首先,将具有测量延时的厚控系统变换为无输出测量延时的系统,再基于变换后的系统构造观测器重构系统状态,然后,基于状态估计设计鲁棒预测控制器。为减小在线计算负担,采用了离线、在线相结合的算法,最后通过实例仿真验证了所提出控制算法的有效性。
二、再论不等式(α+(1/α))(b+(1/b))≥25/4的推广(论文开题报告)
(1)论文研究背景及目的
此处内容要求:
首先简单简介论文所研究问题的基本概念和背景,再而简单明了地指出论文所要研究解决的具体问题,并提出你的论文准备的观点或解决方法。
写法范例:
本文主要提出一款精简64位RISC处理器存储管理单元结构并详细分析其设计过程。在该MMU结构中,TLB采用叁个分离的TLB,TLB采用基于内容查找的相联存储器并行查找,支持粗粒度为64KB和细粒度为4KB两种页面大小,采用多级分层页表结构映射地址空间,并详细论述了四级页表转换过程,TLB结构组织等。该MMU结构将作为该处理器存储系统实现的一个重要组成部分。
(2)本文研究方法
调查法:该方法是有目的、有系统的搜集有关研究对象的具体信息。
观察法:用自己的感官和辅助工具直接观察研究对象从而得到有关信息。
实验法:通过主支变革、控制研究对象来发现与确认事物间的因果关系。
文献研究法:通过调查文献来获得资料,从而全面的、正确的了解掌握研究方法。
实证研究法:依据现有的科学理论和实践的需要提出设计。
定性分析法:对研究对象进行“质”的方面的研究,这个方法需要计算的数据较少。
定量分析法:通过具体的数字,使人们对研究对象的认识进一步精确化。
跨学科研究法:运用多学科的理论、方法和成果从整体上对某一课题进行研究。
功能分析法:这是社会科学用来分析社会现象的一种方法,从某一功能出发研究多个方面的影响。
模拟法:通过创设一个与原型相似的模型来间接研究原型某种特性的一种形容方法。
三、再论不等式(α+(1/α))(b+(1/b))≥25/4的推广(论文提纲范文)
(2)大型稀疏代数系统的数值求解研究(论文提纲范文)
| 摘要 |
| ABSTRACT |
| 第一章 绪论 |
| 1.1 研究背景和意义 |
| 1.2 研究现状 |
| 1.2.1 线性鞍点问题 |
| 1.2.2 非线性鞍点问题 |
| 1.2.3 代数黎卡提方程 |
| 1.3 本文主要研究内容、方法和创新点 |
| 1.4 本文结构安排 |
| 第二章 基于矩阵分裂技术的相关迭代法研究 |
| 2.1 非对称鞍点问题的修正非线性Uzawa算法 |
| 2.1.1 引言, 概念和性质 |
| 2.1.2 Uzawa类型算法回顾 |
| 2.1.3 新的修正非线性Uzawa算法 |
| 2.1.4 数值算例 |
| 2.2 广义的局部对称和斜对称分裂方法 |
| 2.2.1 引言 |
| 2.2.2 GMLHSS迭代方法及其收敛性分析 |
| 2.2.3 数值算例 |
| 2.3 求解奇异鞍点系统的迭代方法的半收敛性分析 |
| 2.3.1 引言 |
| 2.3.2 非精确Uzawa方法和广义非精确Uzawa方法的半收敛性分析 |
| 2.3.3 GSSOR方法的半收敛性分析 |
| 2.3.4 MLHSS方法的半收敛性分析 |
| 2.4 本章小结 |
| 第三章 求解非对称鞍点问题的相关预处理技术研究 |
| 3.1 广义的块对角及块三角预处理技术 |
| 3.1.1 含参数的精确块对角和块三角预条件子 |
| 3.1.2 广义块对角和块三角预处理矩阵的特征值扰动分析 |
| 3.1.3 数值实验 |
| 3.2 非对称鞍点问题的PPSS和PHSS预处理矩阵的谱分布分析 |
| 3.2.1 引言 |
| 3.2.2 PPSS预条件子和PHSS预条件子 |
| 3.2.3 PPSS和PHSS预处理矩阵的谱性质 |
| 3.2.4 数值实验 |
| 3.3 非对称鞍点问题的SIMPLE预处理矩阵的特征值分析 |
| 3.3.1 引言 |
| 3.3.2 SIMPLE预条件子和SIMPLE(R)迭代法 |
| 3.4 本章小结 |
| 第四章 非线性鞍点问题的数值求解研究 |
| 4.1 一些求解非线性鞍点问题的非精确Uzawa方法 |
| 4.1.1 引言 |
| 4.1.2 概念及性质 |
| 4.1.3 求解非线性鞍点问题的几个非精确Uzawa方法 |
| 4.1.3.1 预条件Uzawa方法 |
| 4.1.3.2 第一个非线性Uzawa方法 |
| 4.1.3.3 第二个非线性Uzawa方法 |
| 4.1.3.4 第三个非线性Uzawa方法 |
| 4.1.4 数值实验 |
| 4.2 本章小结 |
| 第五章 代数黎卡提方程的的迭迭代求解研究 |
| 5.1 求解黎卡提方程的松弛Newton-like方法 |
| 5.1.1 引言 |
| 5.1.2 松弛Newton-like方法 |
| 5.1.3 松弛Newton-like方法的收敛性分析 |
| 5.1.4 数值实验 |
| 5.2 修正Newton-Shamanskii方法和拟Newton-like方法 |
| 5.2.1 修正Newton-Shamanskii方法 |
| 5.2.2 修正Newton-Shamanskii方法的收敛性分析 |
| 5.2.3 拟Newton-like方法 |
| 5.2.4 数值实验 |
| 5.3 本章小结 |
| 第六章 结论 |
| 致谢 |
| 参考文献 |
| 攻读博士学位期间的研究成果 |
(3)一类新的Radon型不等式及其应用(论文提纲范文)
| 1引言 |
| 2 几个引理 |
| 3 Radon型不等式及应用 |
(5)空间飞行器姿态复合控制方法研究(论文提纲范文)
| 摘要 |
| Abstract |
| 目录 |
| 符号 |
| 插图 |
| 表格 |
| 第1章 绪论 |
| 1.1 课题研究的背景与意义 |
| 1.2 空间飞行器姿态控制系统 |
| 1.3 姿态控制主要问题与挑战 |
| 1.4 空间飞行器姿态控制国内外研究现状 |
| 1.4.1 PID控制(Proportional Integral Derivative,PID) |
| 1.4.2 自抗扰控制(Active Disturbance Rejection Control,ADRC) |
| 1.4.3 鲁棒控制(Robust Control,RC) |
| 1.4.4 最优控制(Optimal Control,OC) |
| 1.4.5 自适应控制(Adaptive Control,AC) |
| 1.4.6 滑模控制(Sliding Mode Control,SMC) |
| 1.4.7 有限时间控制(Finite-time Control,FTC) |
| 1.5 本文的主要工作及内容安排 |
| 第2章 空间飞行器姿态数学模型 |
| 2.1 引言 |
| 2.2 参考坐标系 |
| 2.3 姿态描述 |
| 2.3.1 方向余弦描述法 |
| 2.3.2 欧拉角描述法 |
| 2.3.3 Rodrigues参数描述法 |
| 2.3.4 四元数描述法 |
| 2.4 空间飞行器姿态运动学方程 |
| 2.5 空间飞行器姿态动力学方程 |
| 2.6 基本引理、性质和定义 |
| 2.7 结论 |
| 第3章 基于滑模和观测器的空间飞行器姿态跟踪控制 |
| 3.1 引言 |
| 3.2 问题描述 |
| 3.2.1 空间飞行器姿态误差动力学和运动学系统模型 |
| 3.3 滑模和观测器控制方案设计 |
| 3.3.1 基于滑模和扩张状态观测器的控制方案设计 |
| 3.3.2 基于滑模和微分观测器的控制方案设计 |
| 3.4 主要结果 |
| 3.4.1 无执行器饱和情况下强抗扰性分析 |
| 3.4.2 执行器饱和情况下强抗扰性分析 |
| 3.5 仿真与分析 |
| 3.5.1 无执行器饱和情况下的仿真结果 |
| 3.5.2 执行器饱和情况下的仿真结果 |
| 3.6 结论 |
| 第4章 基于非奇异终端滑模的空间飞行器有限时间姿态稳定控制 |
| 4.1 引言 |
| 4.2 问题描述 |
| 4.3 基于非奇异终端滑模的有限时间控制方案设计 |
| 4.3.1 非奇异终端滑模面设计 |
| 4.3.2 鲁棒非奇异终端滑模有限时间控制方案 |
| 4.3.3 自适应非奇异终端滑模有限时间控制方案 |
| 4.4 仿真与分析 |
| 4.4.1 鲁棒非奇异终端滑模控制方案的仿真结果 |
| 4.4.2 自适应非奇异终端滑模控制方案的仿真结果 |
| 4.5 结论 |
| 第5章 基于快速非奇异终端滑模的空间飞行器有限时间姿态跟踪控制 |
| 5.1 引言 |
| 5.2 问题描述 |
| 5.3 基于快速非奇异终端滑模的有限时间控制方案设计 |
| 5.3.1 快速非奇异终端滑模面设计 |
| 5.3.2 自适应快速非奇异终端滑模有限时间控制方案 |
| 5.4 仿真与分析 |
| 5.4.1 提出的姿态跟踪控制方案的数值仿真 |
| 5.4.2 不同控制器之间的比较结果 |
| 5.4.3 Rest-to-Rest再定位/机动任务的数值仿真 |
| 5.5 结论 |
| 第6章 基于自适应增益Super-twisting算法的空间飞行器有限时间姿态控制 |
| 6.1 引言 |
| 6.2 问题描述 |
| 6.3 基于Super-twisting算法的有限时间控制方案设计 |
| 6.4 主要结果 |
| 6.5 仿真与分析 |
| 6.5.1 姿态跟踪情况下的数值仿真 |
| 6.5.2 姿态稳定情况下的数值仿真 |
| 6.6 结论 |
| 第7章 基于快速非奇异终端滑模的空间飞行器有限时间容错姿态控制 |
| 7.1 引言 |
| 7.2 空间飞行器姿态稳定容错控制研究 |
| 7.2.1 问题描述 |
| 7.2.2 鲁棒快速终端滑模有限时间姿态稳定容错控制方案设计 |
| 7.2.3 自适应快速终端滑模有限时间姿态稳定容错控制方案设计 |
| 7.2.4 修正自适应快速终端滑模有限时间姿态稳定容错控制方案设计 |
| 7.2.5 仿真与分析 |
| 7.3 空间飞行器姿态跟踪容错控制研究 |
| 7.3.1 问题描述 |
| 7.3.2 自适应快速终端滑模有限时间姿态跟踪容错控制方案设计 |
| 7.3.3 主要结果 |
| 7.3.4 仿真与分析 |
| 7.4 结论 |
| 第8章 结论与展望 |
| 8.1 研究工作的总结 |
| 8.2 研究展望 |
| 参考文献 |
| 攻读博士学位期间发表与撰写的学术论文 |
| 致谢 |
| 作者简介 |
(6)关于图的拓扑不变量和结构性质的几个问题(论文提纲范文)
| 摘要 |
| Abstract |
| 常用记号说明 |
| 第一章 绪论 |
| 1.1 基本概念和符号 |
| 1.2 研究背景与进展 |
| 1.3 图的拓扑指标 |
| 1.4 本文涉及的问题及进展 |
| 1.4.1 图的极大边连通性 |
| 1.4.2 图的[Q,k]-分解问题 |
| 1.4.3 图的Co-PI谱结构 |
| 1.4.4 图的可Q-最大最小化问题 |
| 1.4.5 拓扑不变量和线图 |
| 1.5 本文的组织结构 |
| 第二章 图的极大边连通性 |
| 2.1 参数α∈(-∞,-1]的情形 |
| 2.1.1 预备引理 |
| 2.1.2 定理2.1.1和定理2.1.3的证明 |
| 2.2 参数α∈(0,1)的情形 |
| 2.2.1 定理2.2.1的证明 |
| 2.2.2 定理2.2.2的证明 |
| 2.3 尚待解决的问题 |
| 第三章 关于图的[Q,k]-分解问题的研究 |
| 3.1 [H,2]~τ-分解问题 |
| 3.1.1 H-指标的界 |
| 3.1.2 [H,2]~τ-分解问题 |
| 3.1.3 尚待解决的问题 |
| 3.2 [WW,k]-分解问题 |
| 3.2.1 预备引理 |
| 3.2.2 WW-指标的界 |
| 3.2.3 [WW,3]-分解问题 |
| 3.2.4 尚待解决的问题 |
| 3.3 [R_α~0,k]-分解问题 |
| 3.3.1 预备引理 |
| 3.3.2 [R_α~0,k]-分解问题 |
| 3.3.3 [Z_1,2]-和[Z_2,2]-分解问题 |
| 3.4 [RDD_+,k]-和[RDD_*,k]-分解问题 |
| 3.5 [χ_α,2]-分解问题 |
| 3.5.1 χ_α-指标的界 |
| 3.5.2 [χ_α,2]-分解问题 |
| 第四章 图的Co-PI谱结构 |
| 4.1 Co-PI指标的等价定义 |
| 4.2 Co-PI矩阵及特征值 |
| 4.3 运算图的Co-PI指标 |
| 第五章 图的可Q-最大最小化问题 |
| 5.1 匹配数给定的可RDD_+-最大化问题 |
| 5.2 匹配数给定的可RDD_*-最大化问题 |
| 5.2.1 RDD_*-指标的界 |
| 5.2.2 匹配数给定的可RDD_+-最大化问题 |
| 5.3 独立数给定的可RDD_*-最大化问题 |
| 5.4 连通度给定的可RDD_*-最大化问题 |
| 第六章 拓扑不变量和线图 |
| 6.1 图L[S(T_(n,k))]的拓扑指标 |
| 6.2 图L[S(W_(n+1))]的拓扑指标 |
| 6.3 图L[S(L_n)]的拓扑指标 |
| 第七章 本文总结 |
| 参考文献 |
| 基本概念与主要结果索引 |
| 攻读博士学位期间的研究成果 |
| 致谢 |
| 作者简介 |
| 北京理工大学简介 |
(7)非线性系统的广义张量方法(论文提纲范文)
| 摘要 |
| Abstract |
| 第一章 引言 |
| 1.1 背景 |
| 1.2 相关理论 |
| 1.2.1 张量 (Tensors) |
| 1.2.2 HSS迭代 |
| 1.3 问题的提出 |
| 1.3.1 牛顿法 |
| 1.3.2 传统的张量法 |
| 1.4 广义张量方法 |
| 第二章 三类Tensor系统 |
| 2.1 求解第一类弱非线性张量方程 |
| 2.1.1 Newton-HSS方法 |
| 2.1.2 Picard-HSS方法 |
| 2.1.3 非线性HSS类方法 |
| 2.1.4 数值实验 |
| 2.2 求解第二类M-方程 |
| 2.2.1 HSS型不动点方法 (HSS-F方法) |
| 2.2.2 HSS型动态方法 (HSS-D方法) |
| 2.2.3 数值实验 |
| 2.3 第三类非齐次M-方程根的存在唯一性 |
| 第三章 广义张量方法求解非线性问题 |
| 3.1 问题分析 |
| 3.2 收敛性分析 |
| 3.3 数值实验 |
| 第四章 总结与展望 |
| 4.1 总结 |
| 4.2 展望 |
| 参考文献 |
| 致谢 |
| 研究成果 |
(8)系统辨识(3):辨识精度与辨识基本问题(论文提纲范文)
| 0 引言 |
| 1 辨识精度 |
| 1.1 物理量辨识 |
| 1.2 系统外特性辨识 |
| 2 辨识的基本问题 |
| 2.1 辨识方法的提出 |
| 2.2 辨识输入信号设计 |
| 2.3 可辨识性问题 |
| 2.3.1 参数可辨识性与系统可辨识性 |
| 2.3.2 可辨识性与辨识算法的关系 |
| 2.3.3 开环可辨识性与闭环可辨识性 |
| 2.3.4 可辨识性与能控性和能观测性的关系 |
| 2.3.5 可辨识性与输入信号之间的关系 |
| 2.4 辨识算法的收敛性能 |
| 3 激励信号与激励条件 |
| 3.1 持续激励信号 |
| 1) 有限脉冲响应模型 |
| 2) 受控自回归模型 |
| 3.2 弱持续激励信号 |
| 3.3 衰减激励信号 |
| 3.4 持续激励信号的产生 |
| 3.4.1 白噪声激励信号 |
| 3.4.2 白噪声的产生方法 |
| 3.5 基本激励条件 |
| 3.5.1 强持续激励条件 |
| 1) 强持续激励条件1 |
| 2) 强持续激励条件2 |
| 3) 强持续激励条件3 |
| 4) 广义强持续激励条件1 |
| 5) 广义强持续激励条件2 |
| 6) 广义强持续激励条件3 |
| 3.5.2 弱持续激励条件 |
| 1) 弱持续激励条件1 |
| 2) 弱持续激励条件2 |
| 3) 弱持续激励条件3 |
| 4) 广义弱持续激励条件1 |
| 5) 广义弱持续激励条件2 |
| 6) 广义弱持续激励条件3 |
| 3.5.3 衰减激励条件 |
| 1) 衰减激励条件1 |
| 2) 衰减激励条件2 |
| 3.5.4 其他激励条件 |
| 4 参数估计性质及分析工具 |
| 4.1 参数估计的统计性质 |
| 1) 无偏性 (unbiasness) |
| 2) 渐近无偏性 (asymptotical unbias) |
| 3) 一致性 (consistency) |
| 4) 均方收敛性 (mean square convergence) |
| 5) 有效性 |
| 4.2 Cramér-Rao不等式 |
| 4.3 实用有界收敛性 |
| 1) 一致收敛性 (consistent converegnce) |
| 2) 有界收敛性 (bounded converegnce) |
| 3) 一般收敛性 (general convergence) |
| 4.4 收敛性分析的基本工具 |
| 5 典型辨识算法的收敛定理 |
| 5.1 线性回归模型 |
| 5.1.1 递推最小二乘算法 |
| 1) 基本算法 |
| 2) 递推最小二乘算法的计算量 |
| 3) 递推最小二乘算法计算步骤 |
| 4) 收敛定理 |
| 5.1.2 随机梯度辨识算法 |
| 5.2 伪线性回归模型Ⅰ |
| 5.2.1 递推增广最小二乘算法 |
| 5.2.2 增广随机梯度辨识算法 |
| 1) 基于残差的ESG算法 |
| 2) 基于新息的ESG算法 |
| 5.3 伪线性回归模型Ⅱ |
| 5.3.1 辅助模型递推最小二乘算法 |
| 5.3.2 辅助模型随机梯度辨识算法 |
| 5.4 伪线性回归模型Ⅲ |
| 6 结语 |
(9)忆阻系统的同步及其控制研究(论文提纲范文)
| 摘要 |
| Abstract |
| 第一章 绪论 |
| 1.1 研究背景及意义 |
| 1.2 忆阻的研究进展 |
| 1.3 预备知识 |
| 1.4 本文主要工作与章节安排 |
| 第二章 六个忆阻Lorenz系统的双复合同步 |
| 2.1 引言 |
| 2.2 双复合同步误差设计 |
| 2.3 六个忆阻系统的双复合同步 |
| 2.4 数值仿真 |
| 2.5 结论 |
| 第三章 基于忆阻Lorenz系统的时滞随机混沌系统的混合控制 |
| 3.1 引言 |
| 3.2 预备知识 |
| 3.3 主要结果 |
| 3.4 数值仿真 |
| 3.5 本章小结 |
| 第四章 基于间歇随机噪声的非线性系统的镇定与消稳及其在忆阻系统上的应用 |
| 4.1 引言 |
| 4.2 预备知识 |
| 4.3 稳定性与不稳定性定理 |
| 4.4 基于间歇随机扰动的镇定与消稳 |
| 4.5 应用于忆阻系统的镇定 |
| 4.6 数值例子 |
| 4.7 本章小结 |
| 第五章 基于分布脉冲控制的随机时滞忆阻神经网络的指数同步 |
| 5.1 引言 |
| 5.2 问题描述与预备知识 |
| 5.3 主要结果 |
| 5.4 数值例子 |
| 5.5 本章小结 |
| 总结与展望 |
| 参考文献 |
| 攻读博士学位期间的研究成果 |
| 致谢 |
| 附件 |
(10)轧机电液伺服系统的鲁棒自适应输出反馈控制研究(论文提纲范文)
| 摘要 |
| Abstract |
| 第1章 绪论 |
| 1.1 课题背景及研究目的和意义 |
| 1.1.1 课题背景 |
| 1.1.2 研究目的和意义 |
| 1.2 电液伺服控制系统及研究现状 |
| 1.2.1 电液伺服控制系统概述 |
| 1.2.2 电液伺服控制系统的国内外研究现状 |
| 1.3 问题提出和论文主要研究内容 |
| 1.3.1 问题提出 |
| 1.3.2 本文主要研究内容 |
| 第2章 面向控制的轧机电液伺服系统数学模型 |
| 2.1 轧机电液伺服位置系统的动态描述 |
| 2.2 面向控制的轧机电液伺服位置系统的三种数学模型 |
| 2.3 面向控制的轧机液压厚控系统离散时间数学模型 |
| 2.4 本章小结 |
| 第3章 轧机电液伺服位置系统鲁棒输出反馈控制 |
| 3.1 引言 |
| 3.2 问题描述 |
| 3.3 基于未知输入观测器的鲁棒输出反馈控制 |
| 3.4 仿真研究 |
| 3.5 本章小结 |
| 第4章 轧机电液伺服位置系统自适应输出反馈控制 |
| 4.1 引言 |
| 4.2 基于高增益观测器的自适应输出反馈控制 |
| 4.2.1 自适应输出反馈控制器设计 |
| 4.2.2 闭环系统稳定性分析 |
| 4.2.3 仿真研究 |
| 4.3 基于动态高增益观测器的自适应输出反馈控制 |
| 4.3.1 一类不确定非线性系统的自适应输出反馈控制 |
| 4.3.2 闭环系统稳定性分析 |
| 4.3.3 数例仿真 |
| 4.3.4 轧机电液伺服位置系统的自适应输出控制 |
| 4.3.5 仿真研究 |
| 4.4 本章小结 |
| 第5章 考虑输入饱和的鲁棒动态输出反馈控制 |
| 5.1 引言 |
| 5.2 一类不确定非线性系统的鲁棒动态输出反馈控制 |
| 5.2.1 问题描述 |
| 5.2.2 鲁棒动态输出反馈控制器设计 |
| 5.2.3 数例仿真 |
| 5.3 电液伺服位置系统的抗饱和鲁棒动态输出反馈控制 |
| 5.3.1 问题描述 |
| 5.3.2 鲁棒动态输出反馈控制器设计 |
| 5.3.3 抗饱和鲁棒动态输出反馈控制器设计 |
| 5.4 仿真研究 |
| 5.5 本章小结 |
| 第6章 具有测量延时的轧机液压厚控系统的输出反馈鲁棒预测控制 |
| 6.1 引言 |
| 6.2 轧机液压厚控系统输出反馈鲁棒预测控制 |
| 6.2.1 基于观测器的鲁棒输出反馈控制器设计 |
| 6.2.2 输出反馈鲁棒预测控制器设计 |
| 6.3 仿真研究 |
| 6.4 本章小结 |
| 结论 |
| 参考文献 |
| 攻读博士学位期间承担的科研任务与主要成果 |
| 致谢 |
| 作者简介 |
四、再论不等式(α+(1/α))(b+(1/b))≥25/4的推广(论文参考文献)
- [1]2002年全国各地数学高考模拟试题集锦[J]. 中学数学教学参考试题研究组. 中学数学教学参考, 2003(Z1)
- [2]大型稀疏代数系统的数值求解研究[D]. 李建磊. 电子科技大学, 2010(07)
- [3]一类新的Radon型不等式及其应用[J]. 吴善和. 数学的实践与认识, 2006(03)
- [4]Cn中单位多圆柱上一类α型螺形映射齐次展开式第四项的精确估计[J]. 涂智瑜,刘春燕,罗佩,张如庆,蔡金婷,刘小松. 岭南师范学院学报, 2015(06)
- [5]空间飞行器姿态复合控制方法研究[D]. 路坤锋. 北京理工大学, 2014(04)
- [6]关于图的拓扑不变量和结构性质的几个问题[D]. 苏贵福. 北京理工大学, 2014(04)
- [7]非线性系统的广义张量方法[D]. 邓明宇. 华东师范大学, 2020(11)
- [8]系统辨识(3):辨识精度与辨识基本问题[J]. 丁锋. 南京信息工程大学学报(自然科学版), 2011(03)
- [9]忆阻系统的同步及其控制研究[D]. 张波. 华南理工大学, 2016(05)
- [10]轧机电液伺服系统的鲁棒自适应输出反馈控制研究[D]. 李建雄. 燕山大学, 2012(10)
